近日，2024年IEEE国际计算机算术运算研讨会（ARITH）在西班牙马拉加举行。在本届ARITH上，我院EICAS实验室刘伟强教授、陈珂副研究员、陈辉副研究员团队的两篇高水平论文入选。陈辉副研究员及研究生崔子英赴西班牙参加了此次盛会，向国际计算机与集成电路设计算法领域的同行展示了南航最新研究成果。

1 高基广义双曲CORDIC算法

GH-CORDIC（Generalized Hyperbolic Coordinate Rotation Digital Computer）算法即广义双曲坐标旋转数字计算方法，能够直接计算任意固定基的对数和指数函数。它可以广泛地应用于数字信号处理、通信系统以及人工智能算法中，但传统的radix-2 GH-CORDIC需要通过较多的迭代次数才能实现高精度计算，因此主要存在计算延时较长等缺点，限制了其应用范围。

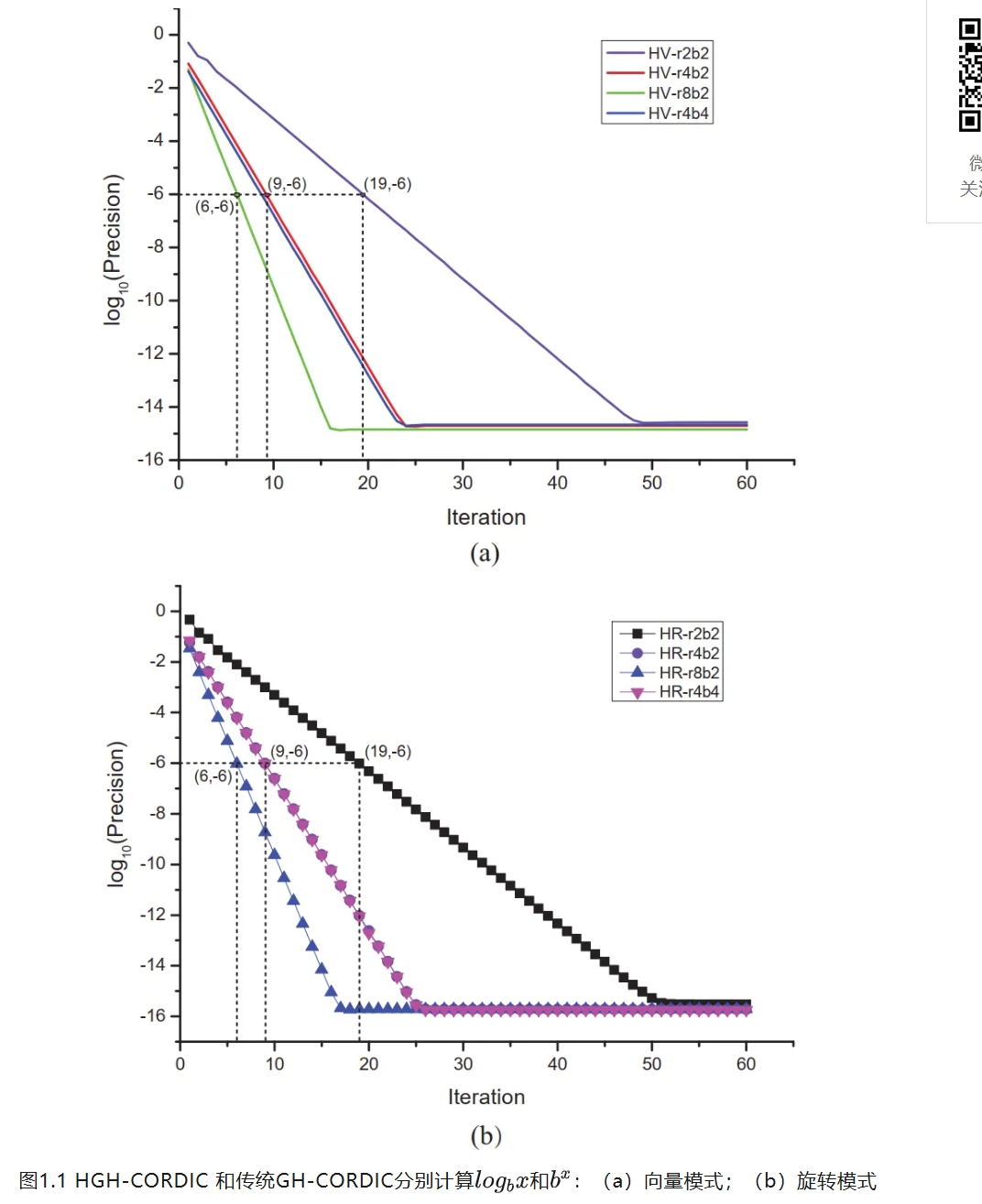
针对上述问题，我院刘伟强教授团队陈辉副研究员提出了一种高基广义双曲CORDIC算法。该算法在保证原计算功能的前提下，可以与radix-2 GH-CORDIC保持同等计算精度，但迭代次数大大减少，且不需要额外的重复迭代次数就可以保证收敛性。该工作首先阐述了高基GH-CORDIC的一般迭代公式，然后证明了其收敛性和迭代方向判定准则，并通过软件仿真验证了理论的正确性，最后还提出了其硬件高效实现的方法。

基于上述算法理论，采用radix-4算法至少可以降低50%的迭代次数，采用radix-8算法至少可以降低66.7%的迭代次数等等。从整体性能角度来说，在设计pipeline架构时，radix-4 GH-CORDIC不仅迭代次数相对较少，而且其硬件面积和功耗开销也可以进一步减少，因此在高精度—高实时系统中具有广泛的应用价值。

该工作以“HGH-CORDIC: A High-Radix Generalized Hyperbolic Coordinate Rotation Digital Computer”为题发表于ARITH，文章的第一作者和宣讲人是我辉副研究员，文章的通讯作者是刘伟强教授。

为了在维持应用精度和性能的情况下降低硬件开销，近似乘法器这一重要计算部件近年来获得了广泛关注。然而，如何在诸多近似乘法器设计中为特定应用选择最佳乘法器一直是一个困难而耗时的工作。

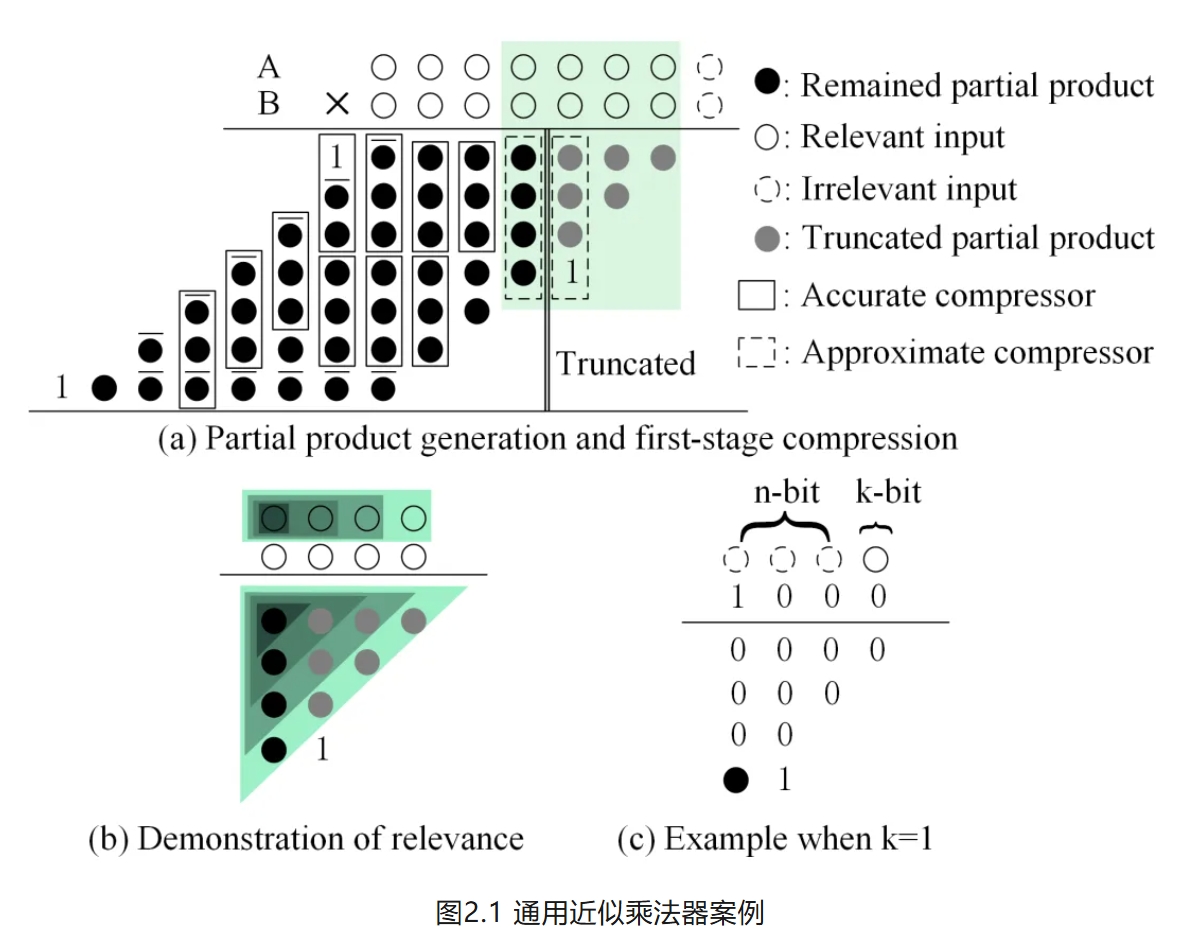
针对上述问题，我院EICAS实验室刘伟强教授、陈珂副研究员团队提出了一种新颖的近似乘法器误差与硬件模型，该模型考虑了输入分布，显著提高了仿真效率。该模型对通用三段式近似乘法器的五种常用误差指标公式进行化简，适用的近似手段包括输入截断与部分积截断，近似编码，近似压缩等。与基于仿真的方法相比，所提出的误差模型仿真时间平均减少了120.85倍，特定情况下可达到2500倍。论文将此模型应用于3*3卷积电路的设计空间探索，与精确模型相比，显著减少了功耗和芯片面积。此外，通过图像应用设计空间探索的任务验证了该模型的实用性。

该工作以A Time Efficient Comprehensive Model of Approximate Multipliers for Design Space Exploration为题，发表于今年ARITH，文章的第一作者是我院硕士生崔子英，文章的通讯作者是陈珂副研究员。